线性回归

1, 模型

模型是指对于某个(类)实际问题的求解或客观事物运行规律进行抽象后的一种形式化表达方式, 可以理解为一个函数(一种映射规则)

任何模型都是由三个部分组成: 目标, 变量和关系. 建模时明确了模型的目标，才能进一步确定影响目标(因变量)的各关键变量(自变量)，进而确定变量之间的关系(函数关系)

通过大量数据检验(训练)模型, 将模型(函数)的各个参数求解, 当参数确定之后, 便可利用模型对未知数据进行求值, 预测

用于训练模型的样本数据中的每个属性称为特征, 用 x 表示, 样本中的每条数据经过模型计算得到的输出值称为标签(监督学习), 用 y 表示, 从而得到 y = f(x) 的函数关系

2, 回归分析

在统计学中, 回归分析指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法

回归分析按照涉及的变量的多少，分为一元回归分析和多元回归分析；按照因变量的多少，可分为简单回归分析和多重回归分析；按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析

回归分析解释自变量 x 发生改变, 因变量 y 会如何改变

拟合 , 插值 和 逼近 是数值分析的三大基础工具. 线性回归和非线性回归, 也叫线性拟合和非线性拟合, 拟合就是从整体上靠近已知点列，构造一种算法(模型或函数), 使得算法能够更加符合真实数据

3, 简单线性回归

线性回归分析的自变量和因变量之间是线性关系, 只有一个自变量时称为 简单线性回归 , 多个自变量时称为 多元线性回归

简单线性回归方程:

$\hat{y}$ 为因变量, x 为自变量, w 为比例关系, b 为截距, w 和 b 就是模型的参数. 例如房屋价格与房屋面积的正比例关系

4, 多元线性回归

现实生活中自变量通常不止一个, 例如影响房屋价格的, 除了房屋面积, 还有交通, 地段, 新旧, 楼层等等因素. 不同的因素对房屋的价格影响力度(权重)不同, 因此使用多个因素来分析房屋的价格(各个因素与房屋价格近似线性关系), 可以得出多元线性回归方程:

$x$: 影响因素, 特征
$w$: 每个 x 的影响力度
$n$: 特征个数
$\hat{y}$: 房屋的预测价格

令:

设 $\vec{w}$ 和 $\vec{x}$ 为两个向量如下:

则方程可表示为:

接下来只需要计算出参数 $\vec{w}^{T}$, 便可以建立模型

5, 损失函数

损失函数, 用来衡量模型预测值与真实值之间的差异的函数, 也称目标函数或代价函数. 损失函数的值越小, 表示预测值与真实值之间的差异越小.

因此, 求解上述模型的参数 $\vec{w}^{T}$, 就是要建立一个关于模型参数的损失函数(以模型参数 $\vec{w}^{T}$ 为自变量的函数), 然而 $\vec{w}^{T}$ 的取值组合是无限的, 目标就是通过机器学习, 求出一组最佳组合, 使得损失函数的值最小

在线性回归中, 使用平方损失函数(最小二乘法), 用 J(w) 表示:

m: 样本(训练集)数据的条数
$y^{(i)}$: 样本第 i 条数据的真实值
$\hat{y}^{(i)}$: 样本第 i 条数据的预测值
$\vec{x}^{(i)}$: 样本第 i 条数据的特征

m, $y^{(i)}$ 和 $\vec{x}^{(i)}$ 已知, 要使 J(w) 最小, 对 $\vec{w}^{T}$ 求导并令导数等于 0 , 便可求得 $\vec{w}^{T}$, 然后将样本(训练集)输入通过机器学习计算出具体的 $\vec{w}^{T}$

6, 回归模型评估

建立模型之后, 模型的效果如何, 需要进行评估, 对于回归模型, 可用如下指标来衡量:

MSE :
平均平方误差, 所有样本数据误差的平方和取均值:

RMSE :
平均平方误差的平方根:

MAE :
平均绝对值误差, 所有样本数据误差的绝对值的和取均值:

上述指标越小越好, 小到什么程度, 不同的对象建立的模型不一样

R² :
决定系数，反应因变量的全部变异能通过回归关系被自变量解释的比例. 如 R²=0.8，则表示回归关系可以解释因变量 80% 的变异. 换句话说，如果我们能控制自变量不变，则因变量的变异程度会减少 80%

在训练集中 R² 取值范围为 [0, 1], 在测试集(未知数据)中, R² 的取值范围为 [-∞, 1], R² 的值越大, 模型拟合越好

R² 的计算公式:

$\bar{y}$: 样本(测试集)的平均值

不管何种对象建立的模型, R² 都是越大模拟越好

例一, 简单线性回归模型: 求鸢尾花花瓣长度和宽度的关系

import numpy as np  

# 导入用于线性回归的类  
from sklearn.linear_model import LinearRegression  

# 切分训练集与测试集的模块  
from sklearn.model_selection import train_test_split  

# 鸢尾花数据集  
from sklearn.datasets import load_iris  

# 设置输出数据的精度为 2 (默认是8)  
np.set_printoptions(precision=2)  

# 获取花瓣长度 x, 宽度 y  
iris = load_iris()  
x, y = iris.data[:, 2].reshape(-1, 1), iris.data[:, 3]  

# 将数据拆分为训练集和测试集, 指定测试集占比 test_size  
# 指定随机种子 random_state(可以任意值但必须确定), 锁定拆分行为  
x_train, x_test, y_train, y_test = train_test_split(  
    x, y, test_size=0.25, random_state=5)  

# 使用训练集训练模型  
lr = LinearRegression()  
lr.fit(x_train, y_train)  

# 求得模型参数  
print('权重 w:', lr.coef_, '截距 b:', lr.intercept_)  

# 调用模型进行预测  
y_hat = lr.predict(x_test)  

# 结果可视化  
import matplotlib.pyplot as plt  

plt.rcParams['font.family'] = 'SimHei'  
plt.rcParams['axes.unicode_minus'] = False  
plt.rcParams['font.size'] = 10  

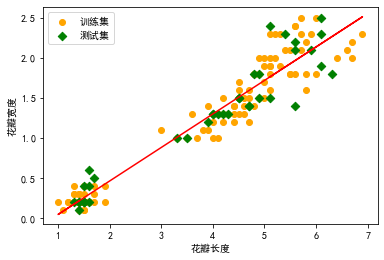
plt.scatter(x_train, y_train, c='orange', label='训练集')  
plt.scatter(x_test, y_test, c='g', marker='D', label='测试集')  
plt.plot(x, lr.predict(x), 'r-')  
plt.legend()  
plt.xlabel('花瓣长度')  
plt.ylabel('花瓣宽度')  
plt.show()  

权重 w: [0.42] 截距 b: -0.370615595909495

# 模型评估  
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score  

print('MSE:', mean_squared_error(y_test, y_hat))  
print('RMSE:', np.sqrt(mean_squared_error(y_test, y_hat)))  
print('MAE:', mean_absolute_error(y_test, y_hat))  
print('训练集R²:', r2_score(y_train, lr.predict(x_train))) # 可换成 lr.score(x_train, y_train)  
print('测试集R²:', r2_score(y_test, y_hat)) # 可换成 lr.score(x_test, y_test)  

MSE: 0.047866747643216113
RMSE: 0.21878470614559903
MAE: 0.1543808898175286
训练集R²: 0.9317841638431329
测试集R²: 0.9119955391492289

列二, 多元线性回归模型: 波士顿房价预测

import numpy as np  
from sklearn.linear_model import LinearRegression  
from sklearn.model_selection import train_test_split  
from sklearn.datasets import load_boston  
import pandas as pd  

boston = load_boston()  
x, y = boston.data, boston.target  
df = pd.DataFrame(np.concatenate([x, y.reshape(-1, 1)], axis=1),   
                 columns=boston.feature_names.tolist() + ['MEDV'])  
# 部分数据  
df.head(3)  

  CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT	MEDV
0	0.00632	18.0	2.31	0.0	0.538	6.575	65.2	4.0900	1.0	296.0	15.3	396.90	4.98	24.0
1	0.02731	0.0	7.07	0.0	0.469	6.421	78.9	4.9671	2.0	242.0	17.8	396.90	9.14	21.6
2	0.02729	0.0	7.07	0.0	0.469	7.185	61.1	4.9671	2.0	242.0	17.8	392.83	4.03	34.7

x_train, x_test, y_train, y_test = train_test_split(  
    x, y, test_size=0.25, random_state=5)  
lr = LinearRegression()  
lr.fit(x_train, y_train)  
print('权重:', lr.coef_)  
print('截距:', lr.intercept_)  
y_hat = lr.predict(x_test)  
print('训练集R²:', lr.score(x_train, y_train))  
print('测试集R²:', lr.score(x_test, y_test))   

# 假如获取了一间房屋的数据, 预测其房价  
room_data = np.array([0.00732, 17.0, 1.31, 1.0, 0.638, 7.575, 62.2, 5.0900,  
                      1.0, 296.0, 15.3, 396.90, 4.98]).reshape(1, -1)  
y_price = lr.predict(room_data)  
print('房屋价格:', y_price)  

权重: [-1.53e-01  4.79e-02 -8.60e-03  2.58e+00 -1.46e+01  3.96e+00 -7.92e-03
 -1.46e+00  3.45e-01 -1.25e-02 -9.19e-01  1.32e-02 -5.17e-01]
截距: 32.214120389743606
训练集R²: 0.7468034208269784
测试集R²: 0.7059096071098042
房屋价格: [33.62]

多元线性回归在空间中, 可表示为一个超平面去拟合空间中的数据点